Laura Bell, Warren Currie (DFO), Stephi Sobek-Swant (rare reserve), John Drake, Wonhyo Lee & Madison Brook (DFO)

ecotheory.ca/theorydata/datatheory.html

1. Epistemology: a brief and idiosyncratic overview
2. Mechanism and novel conditions
3. How can we use models more effectively
   • Focus on mechanism: Predators that benefit their prey (Hine’s Emerald dragonfly)
   • Understand all the model predictions: Regime shifts or transients (Bay of Quinte)
   • Move between mechanistic and data-driven models: Machine learning to suggest mechanism for range limitation (Giant Hogweed)

• reality
• data: a biased subset of reality
• opinion: what we believe about reality
  
  \(\rightarrow\)Science: an attitude linking belief and data, whereby we do not, at least in principle, maintain beliefs that are not supported by data

• We may refer to beliefs supported by data, or which at least do not always contradict data, as theories

• We will like theories to have a few other properties such as:

  • logical consistency
  • coherence with other scientific theories

• Model: a representation of reality

• A structure that:

  • embodies some of our beliefs about reality
    e.g., predators negatively impact prey populations \(\frac{dN}{dt}=f(N)-g(N,P)\)
    
  • mimics some aspect of data
    e.g., linear regression \(y_i=\beta_0+\beta_1x_i+\epsilon\)
    
  • combines these two components (e.g., makes a statement about the expected pattern of data in light of theory
    predator consumption rate can be described as a type II functional response: \(\frac{g(N,P)}{P}=\frac{aN}{N+N_0}\) )

• trade off precision, generality and realism (Levins 1966)
• a model is more specific than a theory, but less detailed than reality
• why? a one-to-one scale map of a city may include all details but is useless as a guide to finding your hotel

“We actually made a map of the country, on the scale of a mile to the mile!”
“Have you used it much?” I enquired.
“It has never been spread out, yet,” said Mein Herr,
“the farmers objected: they said it would cover the whole country, and shut out the sunlight! So we now use the country itself, as its own map, and I assure you it does nearly as well.

Lewis Carroll - The Complete Illustrated Works. Gramercy Books, New York (1982)

• “if we put more details in, it will be a better reflection of reality”
• this syllogism commits fallacy of undistributed middle
• think about the map example: complexity is not necessarily helpful for explanation (e.g., sensitivity analysis)
• complexity is also a bugbear for exploring model assumptions
  
  (e.g., Valle et al. (2009) found that alternate modeling assumptions in the forest stand simulation model SYMFOR can account for 66–97% of the variance in predicted stand dynamics but note that least they COULD do this analysis because the model was not that complex).

• complexity is not necessarily helpful for prediction either

Mayer et al. (2010)

`

• but it fits right??
• no not really: when your model fits your data perfectly, it is unlikely to fit new data well
• overfitting occurs when the data-driven model tries to cover all the data points in the dataset
• as a result, the model starts catching noise and inaccuracies in the dataset

• “if we make it simple, we will capture general principles/effects”
• for data-driven models, underfit happens when your model is not complicated enough
• underfitting introduces bias, such that there is systematic deviation from the true underlying estimator

• Occam’s razor: “entities should not be multiplied beyond necessity”
• simplified descriptions may omit important contingencies
• may also omit time-varying variables, significant effects of environmental stochasticity etc

  “There are two ways of doing calculations in theoretical physics”, he said.
  “One way, and this is the way I prefer, is to have a clear physical picture of the process that you are calculating. The other way is to have a precise and self-consistent mathematical formalism. You have neither.”
  
  Enrico Fermi speaking to Freeman Dyson about pseudoscalar meson theory

• may have significant analysis/implementation issues and no mechanism, in which case the simplicity is self-defeating

1. Explanation
2. Prediction

which absolutely requires mechanism

• “a natural or established process by which something takes place or is brought about”
  OED
• answers the “how” question
• explains the patterns in data by identifying the cause

• something is a “mechanistic model”, because it includes a priori knowledge of ecological processes (rather than patterns)

• e.g., mechanistic niche model based on first principles of biophysics and physiology vs
  
  correlational niche model based on environmental associations derived from analyses of geographic occurrences of species
  (see Peterson et al. 2015 )

• the correlation model is a phenomenological model

• a phenomenological model does not explain why
• simply describes the relationship between input and output
• sometimes, the authors of these models make the assumption that the relationship extends past the measured values
• but of course, that is always a problem (e.g., extrapolation of linear regression beyond input data range)

• and in general it is a spectrum rather than a dichotomy
• particularly true for models at large scale, we will often code small-scale mechanisms as phenomenological components
  
  (i.e., when modelling forest stand dynamics, we will not include a mechanistic description of photosynthesis and evapotranspiration)

• Data-driven: I’m including here standard statistical models (both frequentist and Bayesian), as well as machine learning models

• these models are good at finding patterns

• in the machine learning literature sometimes referred to as the ‘inductive capability’ of algorithms (from past data, one can identify patterns)

• under novel conditions, phenomenological models will not be suitable for prediction (or at least, there is no guarantee they will be)
  \(\rightarrow\) extrapolation problem

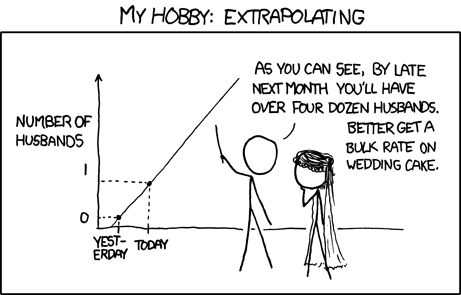
• as a result, one can come to erroneous conclusions

• because these models are based on causal mechanisms rather than correlation, our confidence in extrapolating beyond known data is enhanced (i.e., we can EXPLAIN how that might work)
• that said, there is always uncertainty about how an ecological process will interact with novel conditions

• others disagree
  
  
  
  

  “While mechanistic models provide the causality missing from machine learning approaches, their oversimplified assumptions and extremely specific nature prohibit the universal predictions achievable by machine learning.”
  
  Baker et al. (2018). Mechanistic models versus machine learning, a fight worth fighting for the biological community? Biology Letters, 14(5), 20170660

• truth does not flow from the specific to the universal
  “All swans are white in Austria in 1680”
  
  

does not logically entail
“All swans are white”

• nor does
  
  “All swans are white in Western Europe in 1300”,
  “All swans are white in western Europe in 1301”,
  …..”
  entail
  “All swans are white”
  
• no matter how many specific statements we observe, we are never justified in reasoning to a universal statement (Hume 1739)
• discovery of actual black swans in 1697

• Popper claimed to have refuted the idea that induction provides a foundation for knowledge (Popper, Karl, and David Miller. A Proof of the Impossibility of Inductive Probability. Nature 302, no. 5910 (1983): 687–88.)

• given the success of machine learning, does this mean Popper was wrong that induction is a refuted theory?

• Actually Popper didn’t really “refute” induction, he just noted, that induction only works in the current dataset, not novel conditions

• the “universal predictions” found by data-driven models may not be helpful since they do not include novel conditions
• we can try to use these patterns to predict the future, but we will not be able to explain why our predictions failed or succeeded
• such patterns can be fodder for hypothesizing about mechanism, but they are the START rather than the CONCLUSION of scientific inquiry

• starting from \(\frac{dN}{dt}=f(N)-g(N,P)\) is no different than starting from \(y_i=\beta_0 + f(x_i)+\epsilon\) in terms of mechanism

• we need an explanation or idea about how the predators negatively impact prey population growth rate (what is g(N,P)?)

• we can leave g(N,P) to be a mere description of pattern,
• or we can:
  • examine natural data closely,
  • devise experiments,
  • or reason logically

to develop ideas about mechanism that inform the function

• once the mechanism is specified, the model can predict expected behaviour for given conditions, even when data for those particular conditions do not exist
• do note though that the model has a particular domain of application
  (e.g., “this is a two-species model! it might work okay for agricultural fields, but it will screw up in highly connected communities”)
• on the other hand, when you are aware of the assumptions of the model, you can make guesses regarding the applicability outside of this domain
  (e.g., “true, but the interaction strength between these two species is really large compared to everything else”)

• selection/creation of mathematical and computational models often tends to appeal to classifications rather than mechanism

• a common example is pairwise species interactions such as “predator-prey model”,
  (e.g., Lotka-Volterra pred-prey model \(\frac{dN}{dt}=rN-aNP\))

• “predator-prey” model supposes there is a class of predator-prey interactions that have general properties across species, systems and time that are related to the outcome of the interaction (-/+)

• “classification” models have dubious explanatory and predictive value outside of the exemplar systems in which they were generated

• instead of using classifications of outcomes, we should to focus on incorporating mechanisms, which may generalize across species, systems and time

• for example, while specialist predators may always eat their prey, the net effect of this pairwise species interactions is not fixed

• intuition: we should remove the crayfish because predator-prey models predict decreases in prey density from predation
  
  
  Invasive rusty crayfish eat endangered Hine’s emerald dragonfly larvae (-ve), but also dig burrows that the larvae use for shelter (+ve) (Pintor and Soluk 2006 )

• assume that burrows benefit larvae survival rate by protecting them from drought
• make the same assumption for the predator crayfish
• to obtain

\[ \begin{aligned} &\frac{dN}{dt}=N((a_0+a_1E)-(b_0)N-(c_0)P) \\ &\frac{dP}{dt}=P((f_0+f_1E)-(g_0)P+(h_0)N) \\ &\frac{dE}{dt}=-k(E)+mP \end{aligned} \]

• further assume that burrows decay quickly in the absence of their owner
• find that the engineering predator can have a beneficial impact on its prey,
• increase the equilibrium density if \(a_1m>c_0k\)

• test in model system (burrowing nematodes and E.coli)
• find a positive impact of predators on prey under stressful environmental conditions on the surface of the agar
• and neutral impacts under benign conditions

1. one of the real benefits of using mechanistic models is that they can make predictions you may not expect
2. relying on outcome classifications to both understand and design models precludes understanding all the outcomes of mechanism

• we have had a history of relying on the asymptotic predictions of mechanistic models in tests and predictions (Cuddington 2001)
• transient behaviour is common and important ( Hastings et al. 2018, Francis et al. 2021)
• interactions of model behaviour with time-varying parameters and stochasticity is also common and important (Hastings et al. 2022, Laubmeier et al. 2021)

• history of being increasingly eutrophic
• phosphorus controls implemented 1978
• invaded by zebra mussels in 1994
• meostrophic following this

Bay of Quinte before and after mussel invasion

“In the mid-1990s, zebra and quagga mussels (Dreissena spp.) invaded the area, dramatically changing the water clarity because of the filter-feeding capacity.”

Bay of Quinte remedial action plant (2017)

• a “sudden” change in state, e.g., Scheffer (2001) \(\frac{dx}{dt}=\frac{hx^\rho}{x^\rho+c}-b x+a\)
• lake system moves from phytoplankton-dominated, eutrophic green water state to macrophyte-dominated, oligotrophic state
  Francis et al. (2021)
  `

1. Erode stability of current equilibrium, or
2. Push system to second stable basin with a disturbance

-asymptotic vs transient dynamics predicted by models

`

• all of which arise from the SAME mechanistic model

  1. a regime shift to a 2nd stable state caused by the disturbance of the zebra mussel invasions
  2. a long transient following the erosion of the stability of the eutrophic state because of a lingering ghost attractor
  3. there was just a slow change in phosphorus (i.e. the system does not have bistable dynamics for the relevant parameter values)

• use time-series of potential drivers (total phosphorus (TP), and mussels), and responses (water clarity, chla)
• Linear breakpoint analysis \(E(y_i)=β_0+break_i+x_i\)
• Nonlinear analysis: Use generalized additive model (GAM: \(E(y_i)=β_0+f(x_i)\)), and examine the first derivative of fitted smooth to find periods of rapid change

• global smooth for TP
• explains most of the variation

`

1. the parameter values are in a regime such that there is no sudden change
2. the parameter values DO allow sudden change, but there is a long transient before that change

• in either case, Zebra mussels only likely to contribute as a small scale disturbance

1. there are all kinds of dynamic behaviours predicted by even very simple mechanistic models (e.g., transients can be very long)
2. it is going to be tough to determine mechanism in light of this variety of behaviour…but we NEED to because of management question
3. support analysis with a variety of data-driven models at different temporal and spatial scales

• mechanistic models need testing, for this we use data-driven models
• data-driven models need explaining, for this we use mechanistic models

• use experimental data to suggest candidate predictors: may require cold stratification, refer moist sites

• initial Maxent model to find strong candidates and eliminate correlated predictors (normally we would leave these in and assume that the penalization would take care of overfitting)

`

Madueño 2016

`

`

• final set of simple maxent models, and related statistical model….

`

1. we can use data-driven modelling to identify mechanism
   • requirements for cold seed stratification temperatures to break dormancy
   • with moisture requirements?
2. this use of a data-driven model does require constraints, previous experiment, and some logical connections

Let’s use models more effectively by:

• Focussing on mechanism
• Understanding all the model predictions
• Moving between mechanistic and data-driven models

• providing data, source code and dynamic documents to make work completely reproducible
• these slides can be seen at https:/ecotheory.ca/theorydata/datatheory.html
• document and figures provided at https:/github.com/kcudding/theorydata

The Quinte project is funded by the Department of Fisheries and Oceans Canada. The Hines Emerald dragonfly and Giant Hogweed project was funded by NSERC and Faculty of Science, University of Waterloo.